シニアニンジャの質問「太陽の周りを楕円(だえん)起動する地球をアニメーションしたい」
楕円を描くには、中学生以上(令和では高校からとの事)で学ぶ三角関数という計算式を使います。サイン(sin)やコサイン(cos)という名前は小学生ニンジャでも見たことがあるかもしれません。ほとんどの大人は勉強したけれど、実際に計算したことはないという人が多いのではないでしょうか。
しかーし、プログラマーを目指すニンジャには必要な知識なのです!
一緒にトライしてみましょう。
X座標とY座標を駆使して円を描きます
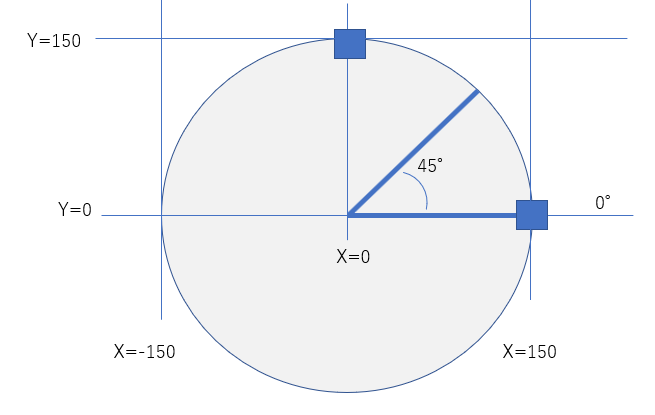
最初は円を書きます。右側の開始地点の角度は「ゼロ度」です。スクラッチャーの皆さんにはショックかもしれませんが三角関数を勉強するときの角度は「0°」なのです。
そして次の三角関数の計算式を使って、角度を[0]度から[360]度まで[1]度ずつ変えて、X座標とY座標を計算します。下図の場合、半径は[150]です。
X座標 = 半径 x cos 角度
Y座標 = 半径 x sin 角度
まずは円軌道のサンプルから試しましょう
初期設定です
- 旗が押されたとき
- 地球の大きさを[50]にする
- 回転方法を[回転しない]にする
- 変数[半径]を[150]にする
- 変数[角度]を[0]にする
- X座標を[ ]、Y座標を[ ]にする
xとyに何を定義しますか? 上図を参考に考えてみてください
繰り返し処理です
- [360]回繰り返す
- X座標を[ ]にする …三角関数の計算式を参照する
- Y座標を[ ]にする
- 角度を[ ]ずつ変える
ここまで地球がぐるっと円の軌道を動きます。下図サンプルを見ないで考えてみてください
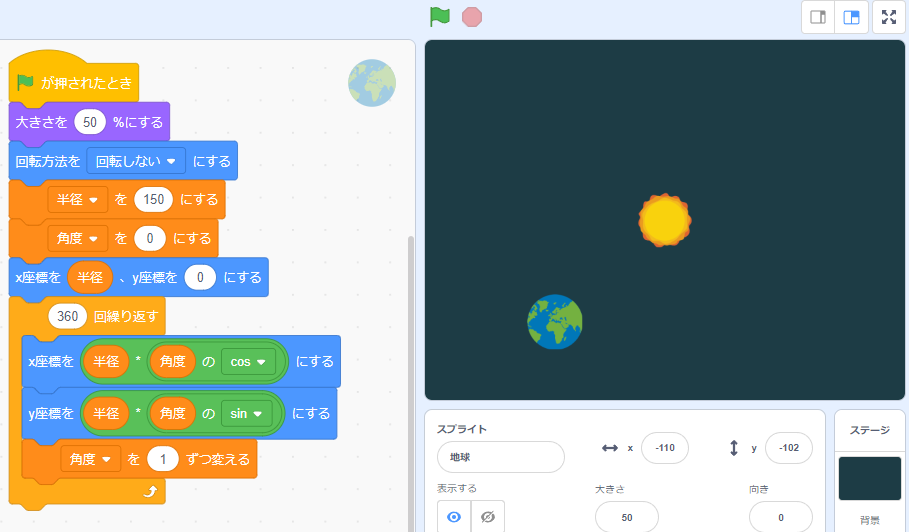
コンピュータではかけ算を[*]、わり算を[/]という記号を使います。
「(角度)の cos 」という式は、学校で「 cos 角度 」と習います。
今度は楕円軌道のサンプルを作ります
円は半径が一つでした。楕円は横幅と縦幅の2つの半径を使います(半径R1と半径R2とします)。下記の楕円の計算式を使います。
X座標 = 半径R1 x cos 角度
Y座標 = 半径R2 x sin 角度
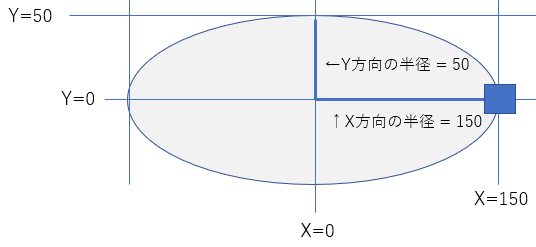
地球が楕円の軌道を動きます。下図サンプルを見ないで考えてみてください
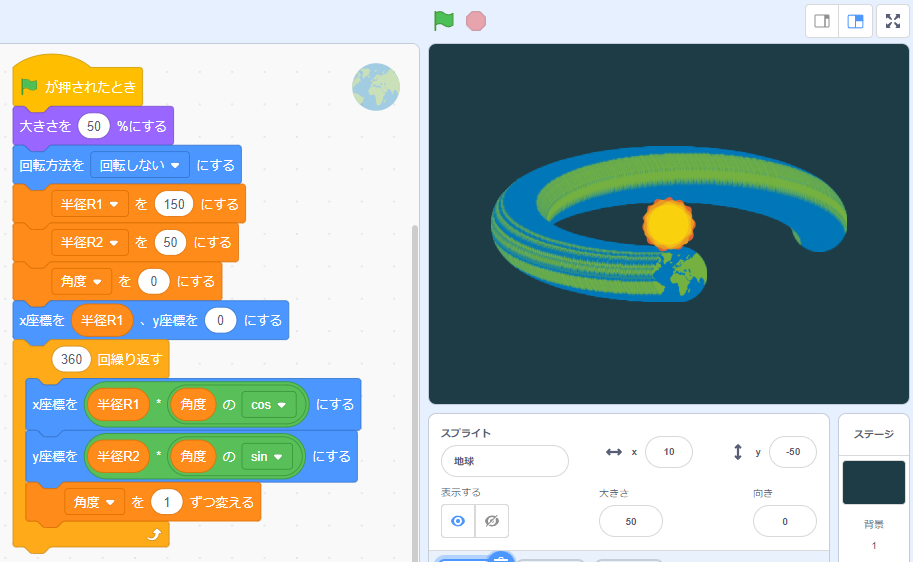
楕円を描きました。この楕円を少しだけ斜めに傾けてみたいです。自分で計算方法を見つけようとしてノートに書いて追加で加える角度や半径などを考えてみましたがギブアップ。検索すると下記の計算式になることがわかりました。自力では一生解けなかった…。変数[角度2]が全体の傾き。
X座標 = 半径R1 x cos 角度1 x cos 角度2 - 半径R2 x sin 角度1 x sin 角度2
Y座標 = 半径R1 x cos 角度1 x sin 角度2 + 半径R2 x sin 角度1 x cos 角度2

パズル並みに難しくなってきましたが、下図サンプルを見ないで考えてみてください
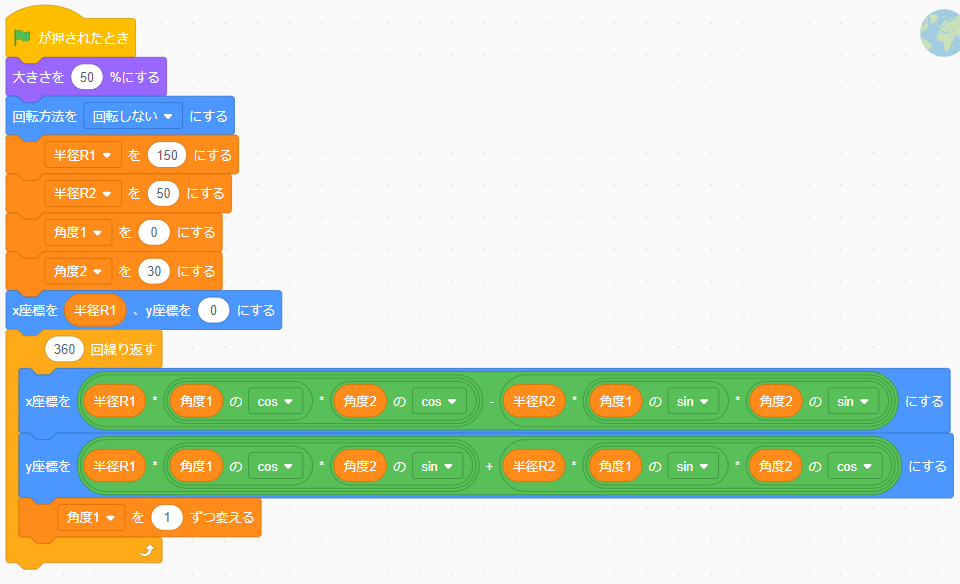
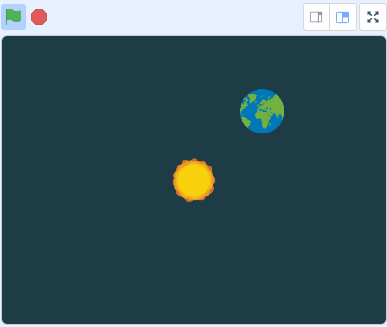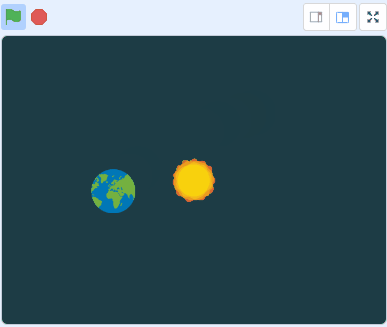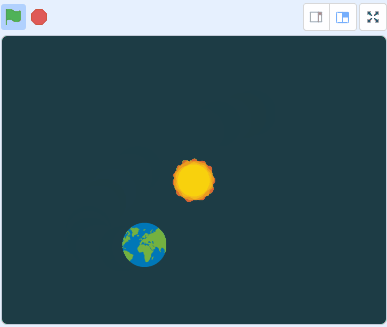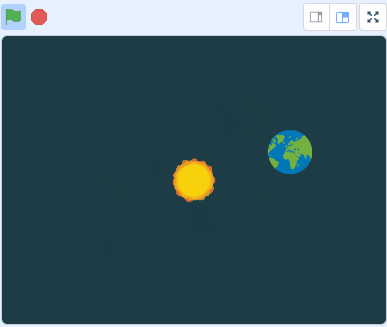
完成したと思ったら、地球の遠近感が足りない。近くは大きく、遠くは小さくしてみよう。

まとめ
楕円軌道に移動するアニメーションができた。シューティングゲームの敵の動きや円錐などグラフィックを描くには必須のスキルです。投石や弓矢などの軌道にもチャレンジしましょうか。
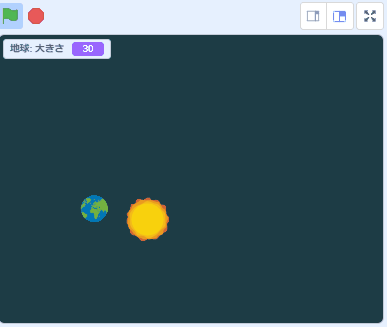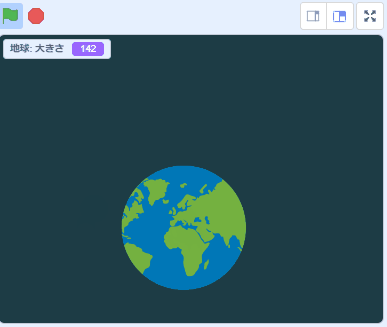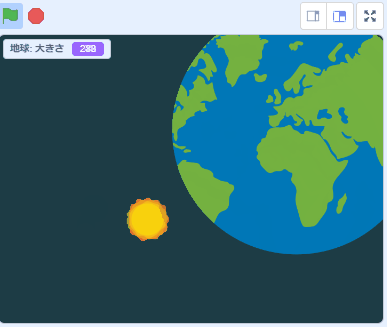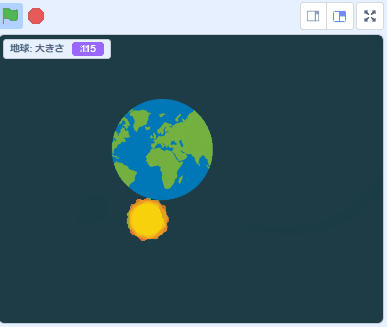
以上です。
楕円が描けると、楕円の半分を使って円錐(えんすい)を描くことができます。